（２）抜取検査とOC曲線

抜取検査では、検査に提出されたロットから一部のサンプルを抜き取って試験し、結果を判定基準と比較してそのロットの合格・不合格を判定します。したがって、それが不適合品でも合格にしてしまう消費者危険と合格品でも不適合と判断してしまう生産者危険があることを認識しなければなりません。

では、どの程度の不適合品を含んだロットがどの程度平均して合格するでしょうか。次のような抜き取り検査を考えてみます。

ロットの大きさ　N = 1000
抜き取った試料の数　n = ２０
合格判定個数 c = 1（ｎ個の試料中に不適合品が、0あるいは１の場合にそのロットは合格、２個以上の場合は不合格）
このロットの不適合率をpとします。

この試料の中にx個の不適合品が出現する確率P(x)は、以下の式で表されます。なお、母集団Nはnに対して十分に大きいとします。実務上サンプルの抜取り比ｎ/Nが1/10ならば、以下の二項分布の式を利用します。

 

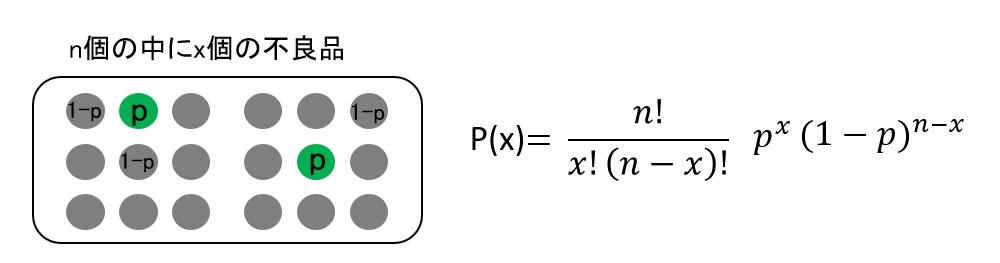
ここでP(x)を試しに計算してみます。上述のｎの元で、p=0.1とし、ｘに数字を代入　していきます。以下のグラフは、母集団Nが1000、抜き取った試料が２０、  この中でｘ個の不適合品が見つかる確率です。なお不適合率pが10％の場合です。横軸はx、縦軸は不適合品がｘ個見つかる確率Ｐ(x)です。

次は、色々とpを変えてみた場合のグラフです。（ｐ=0.01からＰ=0.5まで）

不適合率が５０％だった場合を考えます（半分が不良品！）。取り出す回数nは２０です。不適合品が７個見つかる可能性は7.4%、１０個見つかる可能性は最も大きく17.6%です。半分が不良品で、２０取り出すとしたら１０個が不良品となるのは直感的にもそうかなという気がします。

今度は、横軸を不適合率p、縦軸を不適合品が出現する個数として、確率分布表を作ってみます。代入する式は、先ほどのP(x)です。

この結果をもとに、黄色でハイライト部分をグラフにしてみます。

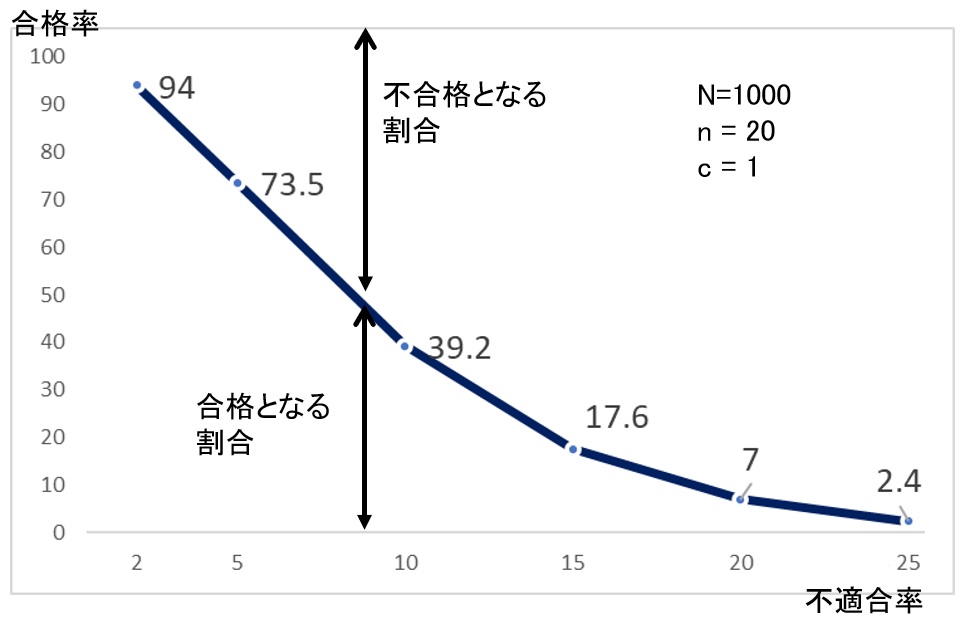
この曲線は不適合率がゼロならば当然１００％の合格率になります。検査に提出されるロットの不適合率が高くなるにしたがって合格率は下がります。

この抜取り検査では、不適合率５％のロットで４回に１回程度の不適合ロットが発生し、不適合率２０％でも１５回に１回程度の割合で合格ロットが発生します。

この曲線は検査特性曲線（OC曲線）と呼ばれ、抜取検査の特性を表します。

次回は、OC曲線から抜取検査の結論を正しく判別することを考えてみたいと思います。