検査会社は提出された試料に対してその特徴等を試験によって明らかにします。しかしながら、その試料が母集団となっているもの全体に対して特徴を正しく表しているかというと、全量検査でない限り必ずしも１対１で対応している訳ではありません。母集団の特徴を推測するために、目的に照らしてどの程度のサンプル試料の量が必要で、どのような方法で採取するか等、正しくサンプリングしなければ、母集団全体の特徴を誤って把握することになってしまいます。本資料では、適切なサンプリング方法を時系列に沿ってその概要を解説したいと思います。

 

【どの程度サンプル数が必要か】

 

サンプリングは、全数検査や全量検査を行わずに母集団に関する正確な情報を効率的に知りたいときに行うものです。すなわち、母集団の情報を得ることがサンプリングの目的です。ですので、知りたい母集団の情報を安価に早く且つ正確に知ることができるのが良いサンプリングといえます。

一般にサンプル数が多くなるとサンプリングの誤差が小さくなり、推定する母集団の情報の精度が良くなります。しかし、サンプル数が多いとその分コストや手間がかかりますので、注意が必要です。したがって、一概にサンプル数が多いほど良いかというと精度とコストのバランスから決まるため、そうではありません。

サンプリング誤差の大きさはサンプル数の平方根に逆比例します。サンプル数を４倍にすると誤差の大きさは１/2になり、9倍にした場合は１/3になります。このようにコストと時間をかけてもサンプリング誤差が思ったほど小さくならない場合があります。

また、サンプルとして必要なグラム数はサンプリング誤差の大きさに影響します。母集団において調査対象となっている成分がどのように分布しているかによりますが、サンプル量を増やすとサンプルリング誤差が小さくなります。例えば穀物のような粒状のサンプルの場合、サンプル量とサンプル数は比例します。

なお、母集団の均一性が高いほどサンプル量のサンプリング誤差への影響は小さくなります。逆にいうと母集団の不均一さが高ければサンプル量を増やさないと必要な精度を得られなくなります。

必要なサンプル数は統計的に求めることができます。決める必要があるのは、どのぐらいの精度を実現したいか（推定の精度）、誤差をどの範囲に収めるか、そして必要になるのは母集団の分散の推定値です。この推定値は普段の品質管理データや予備調査データがあれば、その不偏分散を使います。

 

①　母集団の推定値が平均値の場合

 

 

 

 

ｎは理論的サンプル数、ＣＩは信頼区間、kは意図する推定の精度よって決まる数値（危険率５％の時は1.96（0.95以上の確率で誤差が範囲内に収まっているか判断できる数値））、は母集団の推定値です。

 

②　母集団の推定値が比率の場合

 

 

 

 

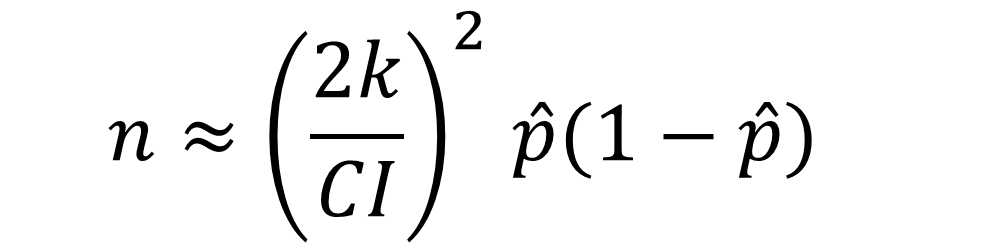
ｎ、ｋ、ＣＩは先ほどの説明と同様です。この式は母集団の大きさがサンプル数よりもはるかに大きい際に使用することができます。

 

あるNonGMOとされるダイズの母集団について遺伝子組換えダイズの検出検査を行ったとします。この母集団について予備実験を行った結果、陽性反応が出た割合が0.9%だったとします。この母集団について陽性反応が出る割合を±２％の精度で知りたいとします。

ｋ＝1.96, CI=2%×２=4% (0.04), =0.9%(0.009)を代入します。すると、

 

 

 

 

よってこの母集団から8６個をランダムサンプリングすれば、陽性反応が出た割合を危険率５％で、それを±２％の精度で知ることができます。

 

次回は、「サンプリングの実施方法について」です。

 

参考資料：

「食品のサンプリングに関するガイダンス」、農研機構食品総合研究所ウェブサイト

鐵 健司(2000). 新版 品質管理のための統計入門 株式会社日科技連出版社

大屋幸輔(2003)コア・テキスト統計学 株式会社サイエンス社